Setelah anda mempelajari tips dan trik mengerjakan soal penerapan himpunan dalam kehidupan sehari-hari, sekarang Mafia Online akan berikan contoh dan latihan soal penerapan himpunan dalam kehidupan sehari-hari. Akan tetapi sebelum anda membaca contoh soal dan mengerjakan soal latihannya alangkah baiknya ada terlebih dahulu menguasai konsep himpunan dan diagram venn serta tips dan trik mengerjakan soal-soal penerapan himpunan dalam kehidupan sehari-hari.
Contoh Soal 1
Dalam suatu kelas terdapat 48 siswa. Mereka memilih dua jenis olahraga yang mereka gemari. Ternyata 29 siswa gemar bermain basket, 27 siswa gemar bermain voli, dan 6 siswa tidak menggemari kedua olahraga tersebut. Gambarlah diagram Venn dari keterangan tersebut dan tentukan banyaknya siswa yang gemar bermain basket dan voli.
Penyelesaiannya:
Gambar diagram Venn dari keterangan tersebut dapat diperoleh jika banyaknya siswa yang gemar bermain basket dan voli diketahui, maka cari terlebih dahulu banyaknya siswa yang gemar bermain basket dan voli:
n{AΛB} = (n{A} + n{B}) - (n{S} - n{X})
n{AΛB} = (n{A} + n{B}) - (n{S} - n{X})
n{AΛB} = (29 + 27) – (48 – 6)
n{AΛB} = 14Siswa yang memilih basket saja = 29 - 14 = 15 orang
Siswa yang memilih voli saja = 27 - 14 = 13 orang
Gambar diagram Venn dari keterangan tersebut adalah
Contoh Soal 2
Pada sebuah kelas yang terdiri atas 46 siswa dilakukan pendataan pilihan ekstrakurikuler. Hasil sementara diperoleh 19 siswa memilih KIR, 23 siswa memilih PMR, dan 16 siswa belum menentukan pilihan. Tentukan banyaknya siswa yang hanya memilih PMR saja dan KIR saja.
Penyelesaiannya:
Siswa yang memilih PMR dan KIR adalah:
n{AΛB} = (n{A} + n{B}) - (n{S} - n{X})
n{AΛB} = (n{A} + n{B}) - (n{S} - n{X})
n{AΛB} = (19 + 23) – (46 – 16)
n{AΛB} = 12
Siswa yang memilih KIR saja = 19 - 12 = 7 orang
Siswa yang memilih PMR saja = 23 - 12 = 11 orang
Jika digambarkan ke dalam diagram venn maka gambarnya seperti dibawah ini.
Siswa yang memilih PMR saja = 23 - 12 = 11 orang
Jadi banyaknya siswa yang hanya memilih PMR saja ada 11 siswa dan KIR saja ada 7 siswa
Contoh Soal 3
Dari 40 siswa dalam suatu kelas, terdapat 30 siswa gemar pelajaran matematika dan 26 siswa gemar pelajaran fisika. Jika 2 siswa tidak gemar dengan kedua pelajaran tersebut, tentukan banyaknya siswa yang gemar pelajaran matematika dan fisika.
Penyelesaiannya:
n{AΛB} = (n{A} + n{B}) - (n{S} - n{X})
n{AΛB} = (30 + 26) - (40 - 2)
n{AΛB} = 56 - 38
n{AΛB} = 18
Jadi banyaknya siswa yang gemar matematika dan fisika ada 18 siswa
Contoh Soal 4
Dari 40 siswa dalam suatu kelas, terdapat 30 siswa gemar pelajaran matematika dan 26 siswa gemar pelajaran fisika. Jika 2 siswa tidak gemar dengan kedua pelajaran tersebut, tentukan banyaknya siswa yang gemar pelajaran matematika dan fisika.
Penyelesaiannya:
n{AΛB} = (n{A} + n{B}) - (n{S} - n{X})
n{AΛB} = (30 + 26) - (40 - 2)
n{AΛB} = 56 - 38
n{AΛB} = 18
Jadi banyaknya siswa yang gemar matematika dan fisika ada 18 siswa
Contoh Soal 4
Dari 50 siswa di suatu kelas, diketahui 25 siswa gemar matematika, 20 siswa gemar fisika, dan 7 siswa gemar kedua-duanya. Tentukan banyaknya siswa yang tidak gemar matematika dan fisika.
Penyelesaiannya:
n{AΛB} = (n{A} + n{B}) - (n{S} - n{X})
7 = (25 + 20) - (50 - n{X})
7 = 45 - 50 + n{X}
7 = - 5 + n{X}
n{X} = 7 + 5
n{X} = 12
Jika digambarkan ke dalam diagram venn maka gambarnya seperti dibawah ini.
Jadi banyaknya siswa yang tidak gemar matematika dan fisika ada 12 siswa
Contoh Soal 5
Dari sekelompok olahragawan, terdapat 18 orang yang gemar bulu tangkis, 16 orang gemar bola basket, dan 12 orang gemar dua-duanya.Gambarlah diagram Venn yang menunjukkan pernyataan di atas dan tentukan jumlah olahragawan tersebut.
Penyelesaiannya:
Gambar diagram Venn yang menunjukkan pernyataan di atas adalah
Jumlah olahragawan tersebut adalah 22 orang
Gambar diagram Venn yang menunjukkan pernyataan di atas adalah
Contoh Soal 6
Siswi-siswi kelas VIIC dan VIID salah satu SMP Negeri di Jakarta mengikuti lomba memasak dan menjahit yang diadakan dalam waktu yang berbeda. Dalam kelas tersebut terdapat 30 orang siswi. Setelah selesai dikelompokkan, 18 orang ikut lomba memasak, 17 orang ikut lomba menjahit, dan 12 orang ikut lomba memasak dan menjahit. Tentukan pernyataan di atas dalam diagram Venn dan hitung berapa siswi yang tidak mengikuti lomba dua-duanya.
Penyelesaiannya:
Gambar diagram Venn yang menunjukkan pernyataan di atas adalah
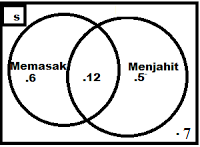jumlah siswi yang tidak gemar dua-duanya ada 7 orang
Contoh soal 1 sampai 6 di atas dapat diselesaikan dengan cara cepat kecuali contoh soal 7 di bawah ini.
Gambar diagram Venn yang menunjukkan pernyataan di atas adalah
Contoh soal 1 sampai 6 di atas dapat diselesaikan dengan cara cepat kecuali contoh soal 7 di bawah ini.
Contoh Soal 7
Suatu kompleks perumahan mempunyai 43 orang warga, 35 orang di antaranya aktif mengikuti kegiatan olahraga, sedangkan sisanya tidak mengikuti kegiatan apa pun. Kegiatan bola voli diikuti 15 orang, tenis diikuti 19 orang, dan catur diikuti 25 orang. Warga yang mengikuti bola voli dan catur sebanyak 12 orang, bola voli dan tenis 7 orang, sedangkan tenis dan catur 9 orang. Tentukan banyaknya warga yang mengikuti ketiga kegiatan olahraga tersebut.
Penyelesaian:
misalkan yang mengikuti ketiga kegiatan olahraga tersebut adalah x maka yang ikut:
voli dan tenis saja = 7-x
tenis dan catur saja = 9-x
voli dan catur saja = 12-x
voli saja = 15 –(12-x)-(7-x)-x = -4+x
tenis saja = 19 –(9-x)-(7-x)-x = 3+x
catur saja = 25 –(9-x)-(12-x)-x = 4+x
maka diagram vennya menjadi:
dari diagram venn di atas yang mengikuti ketiga kegiatan olahraga tersebut adalah
=>> 35 = (7-x) + (9-x) + (12-x) + (-4+x) + (3+x) + (4+x) +x
=>> 35 = 31 +x
=>> x = 4
jadi yang mengikuti ketiga kegiatan olahraga tersebut adalah 4 orangUntuk menjawab contoh soal 1 sampai 6 di atas coba gunakan cara cepat, silahkan baca caranya di postingan Mafia Online yang berjudul "Cara Cepat Mengerjakan Soal Himpunan (Diagram Venn)"